Hello, and welcome to first in a new series I am calling: Sunday school. In this weeks lesson I’m going to be teaching you about some real life physics I encountered on one of my many adventures.

So here’s the story. The other day I went wakeboarding on a lake just north if the French city of Toulouse. It was an incredible experience, something I’ve never done before but will definitely be doing again. Wakeboarding, in case you haven’t heard of it, is a water sport that involves holding onto a rope being pulled whilst you balance on top of a board. The speed of the tope pulling you propels you across the water and you maintain your speed and stability so long as the rope stays taught.

At the place where I took part in this sport, the rope was attached to some overhead pulleys arranged in a rectangle, meaning about four times throughout the path round I had to turn to the right. Here is where I encountered the physics.

Most people are familiar with pythagorous’ theorem but just in case I’ll repeat it here. The Pythagourous theorem is a mathematical rule of right angled triangles. It states that the sum of the squares of the two sides of a right angle triangle (known as the opposite and the adjacent) is equal to the square of the line across (known as the hypotenuse). This equation can be seen here:

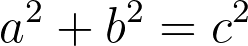
The change of direction for my travelling wasn’t exactly 90 degrees, but it was close enough that the pythagoras equation can be applied. Let’s say that the rope pulling me was 10 metres long. Whilst travelling straight, I stay 10 metres behind the connector and the rope stays taught. But change direction, and the problem changes. For the first few seconds, I keep my velocity forward but the connector is now travelling sideways to me. Putting this into our equation spells trouble.

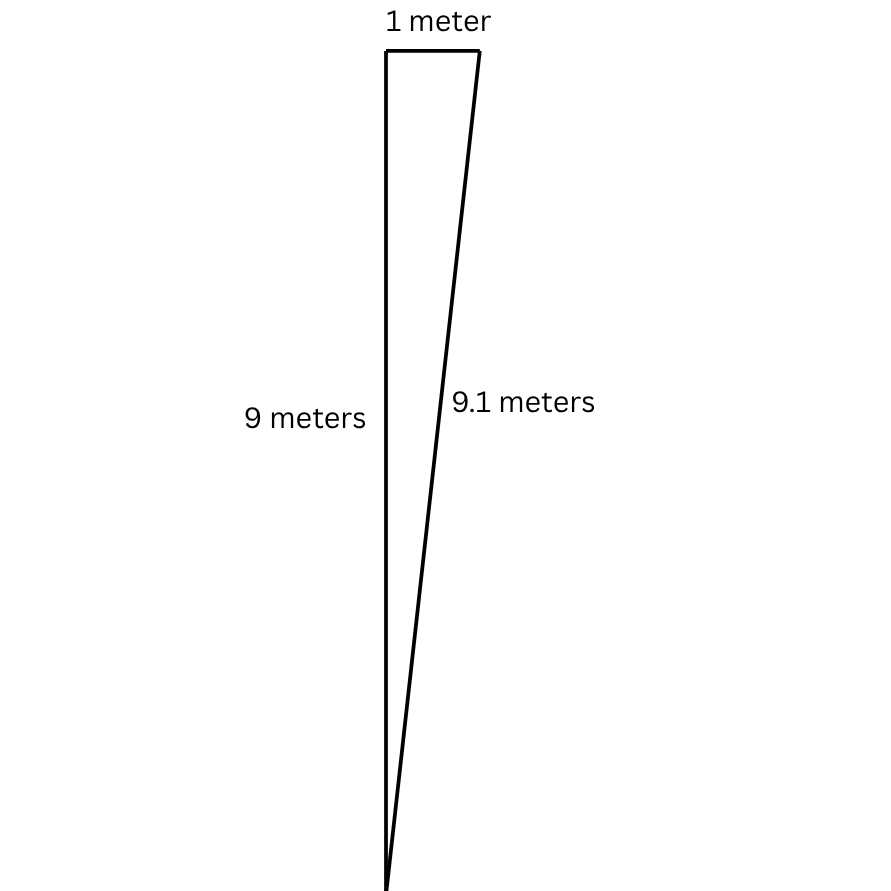
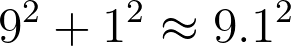
If we both have the same speed, we both travel 1 metre. Pythagoras shows us that the hypotenuse of our triangle works out to only be 9 metres in length. There’s an extra metre of rope between the me and the connector, and so the line has now gone slack.

With no force pulling me, I slow to a stop, but the connector keeps moving. The change in both speed and distance between us increases until once again that hypotenuse equals 10 metres. Once it does…

The rope pulls on me incredibly hard and into the water I go! This is a big problem because I’m a big fan of having my arms attached to my body and my lungs not full of water. After a few more times of falling in the water, I had to properly think of a way of not falling off, and after a bit of thinking I found that mathematics has the solution!

I need to consistently stay around 10 meters behind the connector despite changing directions. The issue is with the rope going slack, so as the connectors moving to the right, I wonder what would happen if I was further over to the left?

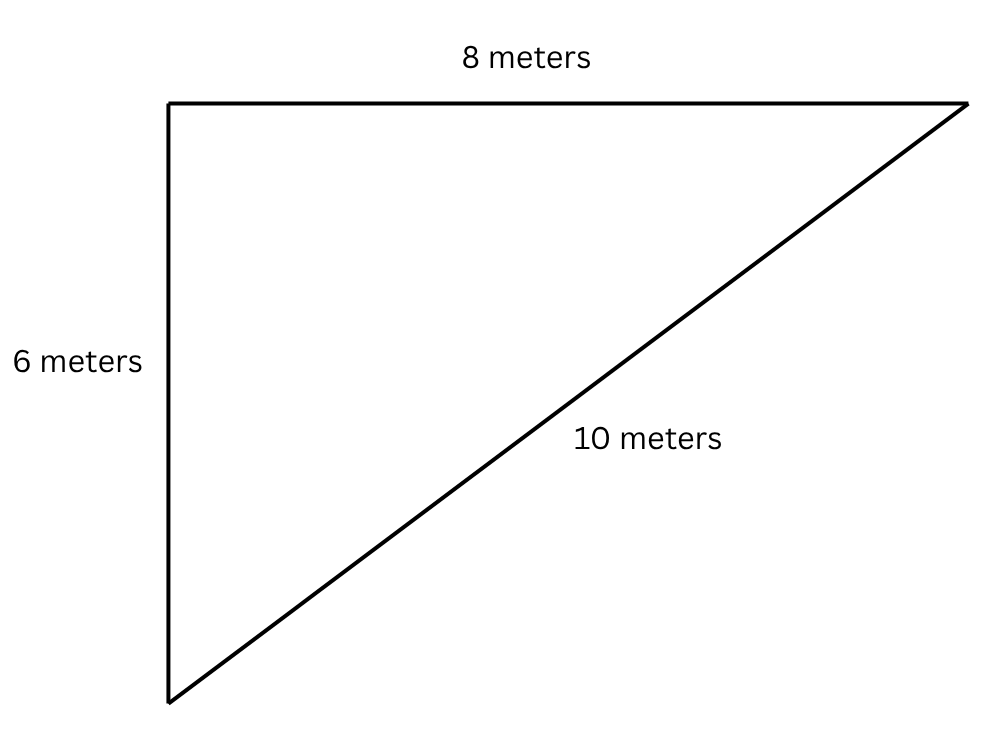
During wakeboarding, by moving the handle I hold to the left and to the right, I can shift my body to the right and to the left. I’m need to always be 10 meters away from the connector, but I can be seven meters behind and seven meters to the left of the connector. The rope will make up the hypotenuse and that will still be 10 meters!

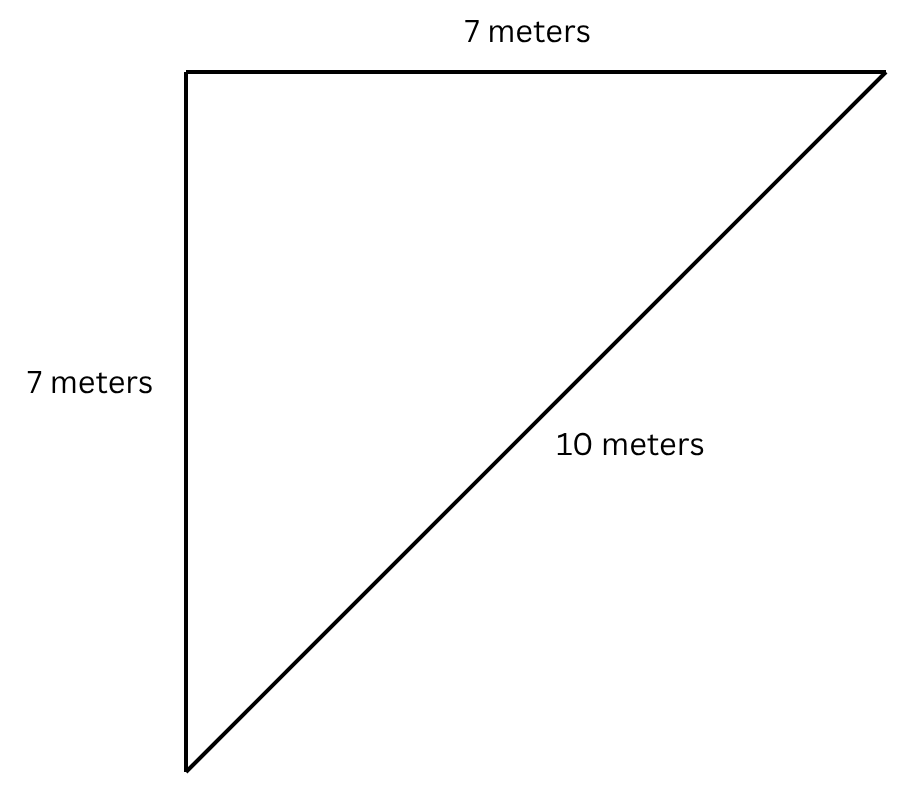
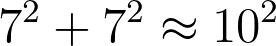
Now, when the connector turns right, I keep my speed from before and go 1 metre forward, but the connector goes 1 meter to the right. I am now 6 metres behind and 8 metres to the left of the connector. Plugging these into the pythagoras equation and we can see that the connector and I are still 10 meters apart, so the line stays taught!

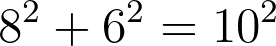
After this, with the line pulling me to the right I gain sideways velocity, but the pythagoras continues to work so long as I take the outside lane. The line stays taught and I don’t get pulled too hard on the board.

I implement my mathematical solution, taking the outside lane. This time, the rope stays taught and I soar around the corner and continue onwards. My wakeboarding adventure continues, and as I travel around the next corner and the next, I hear myself yell:

“Py-f*ing-thagoras”

See you in the next class!

Cassie

P.S. Thanks for reading my first lesson, this is a new series I’m pretty excited about starting. I have always loved teaching and so hope to get a few more lessons here when I have the time so that I’ve got things ready should I need them.

If you enjoyed learning about Pythagorous, or would like to learn abot another subject, leave a comment saying so! It always helps me out to know what people want to read 🙂