Time again for another sunday school lesson! This week I’ve got another lesson on how you can apply mathematics to sports, more specifically: Basketball!

Basketball is a sport that has been around for over 100 years, but sports similar to it such as the Mayan’s ballgame have been around for millenia! I’ll quickly go through the basic premise of the game.

The Rules of the Game

There are two teams in a game of basketball (usually the home and visiting teams), each team is composed of five players who as far as I know don’t have set positions. Each of these players is able to run anywhere in the court but, if they have the basketball, they have to dribble (bounce) it as they run; else they be accused of travelling (moving whilst holding the ball). If a player stops whilst holding the ball, they have to throw it; either to another player as a pass, or towards the net as a shot. How many points a player gets for a shot is dependant on where they throw from.

Surrounding the net is a large D-shaped line known as the three-point-line, so called because if you throw from behind this line, you score three points. Shoot from within the line and you score two points, and in ‘rare’ circumstances when a foul happens and you take a free throw, you only score one point if you make it in. Simple!

The hard part of basketball, is getting the ball into the net. Despite the ball being half the size of the net, from a distance of about 7 meters where the three-point-line stands, that makes no difference. So, making sure any throws you do are accurate is very important!

To start off, lets go for the lowest points, can I throw a basketball into the hoop from the three throw line? At that distance, I’m about 4.6 metres behind the net. The net is about 3 metres off of the ground, and I stand at about 1.8 metres. I’m gonna assume that my arm goes about half a metre above me when I throw so that’s about 2.3 metres. With all of our starting numbers, it’s time do some geometry!

Geometry Time

When I throw the ball, it needs to travel 4.6 metres forward, whilst travelling up and back down so that it’s 0.7 metres above where it started. What I want to know, is just how fast I need to throw the ball and at what angle, so that the ball goes straight in the net.

Things can be simplified even further though! Thrown things get their curve from gravity, the huge force that pulls object on Earth towards the ground. Gravity only works vertically here, so if we seperate the vertical and horizontal movements of the ball we can find some useful values.

The horizontal speed of the ball will stay the exact same throughout the movement, no gravity is acting sideways! So the time taken for the ball to travel the horizontal distance can be worked out from a simple distance divided by speed:

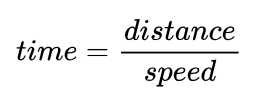
So that’s the horizontal done, but the vertical is a bit more complicated! With gravity acting on the ball, I need to throw the ball much higher so that it then falls back down into the net. Luckily, mathematicians have created great ways of calculating this, in the form of the SUVAT equations!

In these equations, there are five variables to consider:

• s – The displacement or distance travelled
• u – The initial speed or velocity
• v – The final speed or velocity
• a – The acceleration acting
• t – The time taken for everything to happen

Hence, SUVAT. I already have versions of s, u and t from my horizontal equation earlier, so any future equations I use will need to have them. That leaves the other two, v and a. I’m not too bothered about the final speed of the ball I’m throwing, but as gravity is acting on the ball it’ll definitely be useful to include that.

There are five different SUVAT equations you can use depending on your scenario and which variables you are using. As I’ll be using s, u, a and t, I’ll be using this equation:

Now comes the tricky part, I have seperated my problem into two scenarios: the horizontal and the vertical, but the speed is used in both! I need to define my overall speed in terms of the angle I’m throwing it, which as you’ll remember is 45 degrees. I can seperate the speed into horizontal (u_h) and vertical (u_v) as follows:

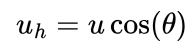
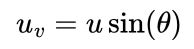
In those equations, θ (theta) is the angle at which I’m throwing the ball. Now I can sub in my equation for the horizontal time into my equation for the vertical distance:

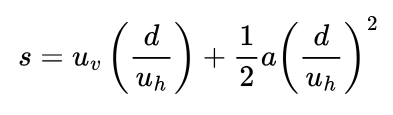
Here, d is the horizontal distance travelled. In total that will be 4.6 metres, but I’ll leave it as d for now and you’ll see why later. There’s just one more thing I need to add, remember this ball is starting out over 2 metres above the ground from where I throw it, so I’m going to add an extra 2.3 metres to my equation to account for that.

Next, we need to simplify. Remember, the only unknown values in my equation are going to be the speed and angle at which I throw the ball. These different velocities, whilst useful, have made a big mess of the equation, so I’m going to sub in for them too:

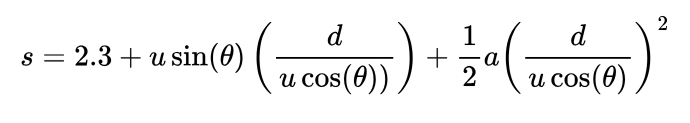
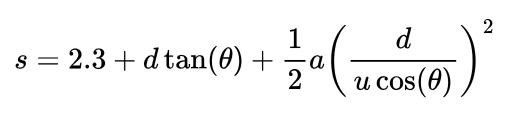
Don’t worry, that’s our last equation! Now we have our way of working it out, don’t we? Maybe you can see the ‘problem’, u and θ are completely inseperable! Luckily, that’s exactly what’s supposed to happen! u is as dependant on θ as θ is dependant on u! Which I think I can demonstrate quite well in the following graph:

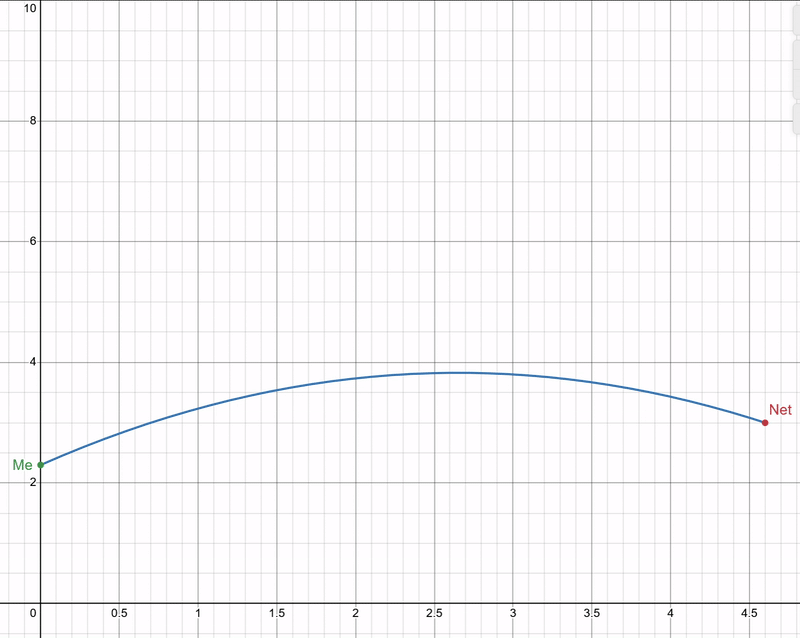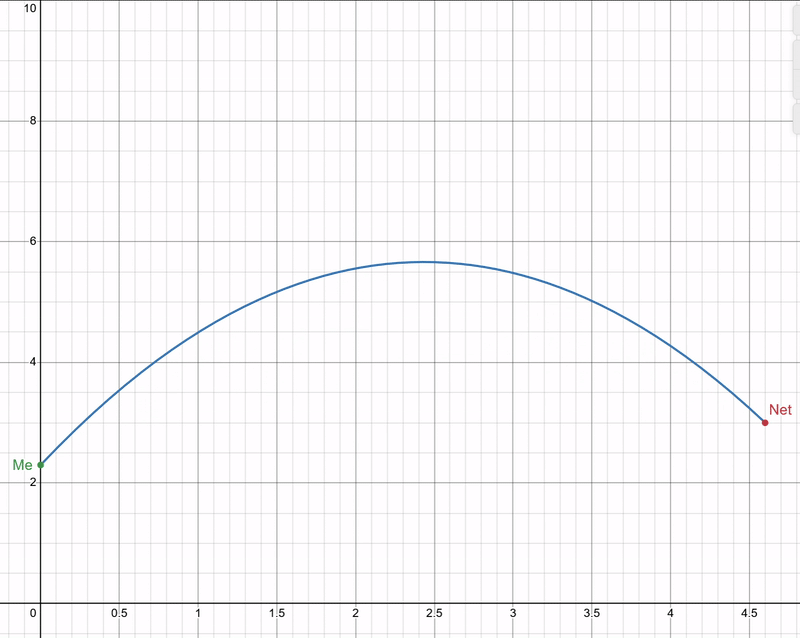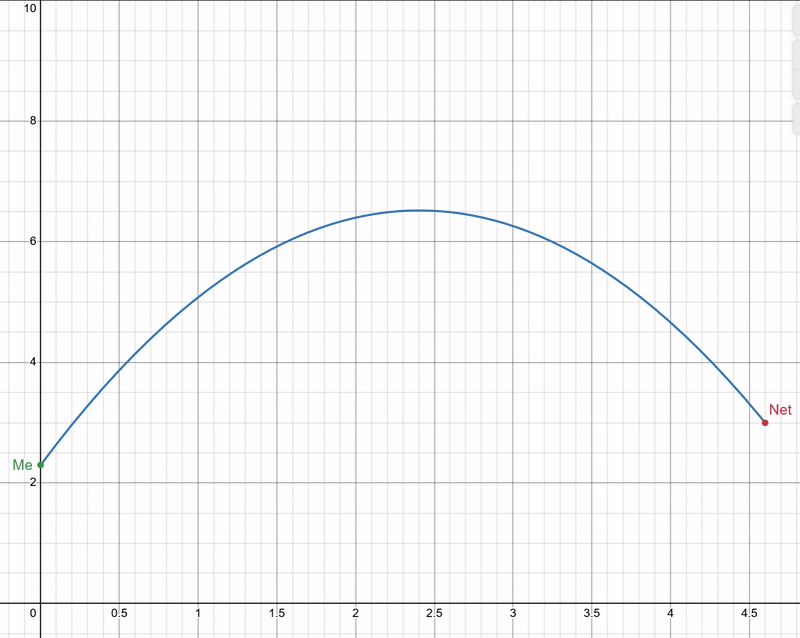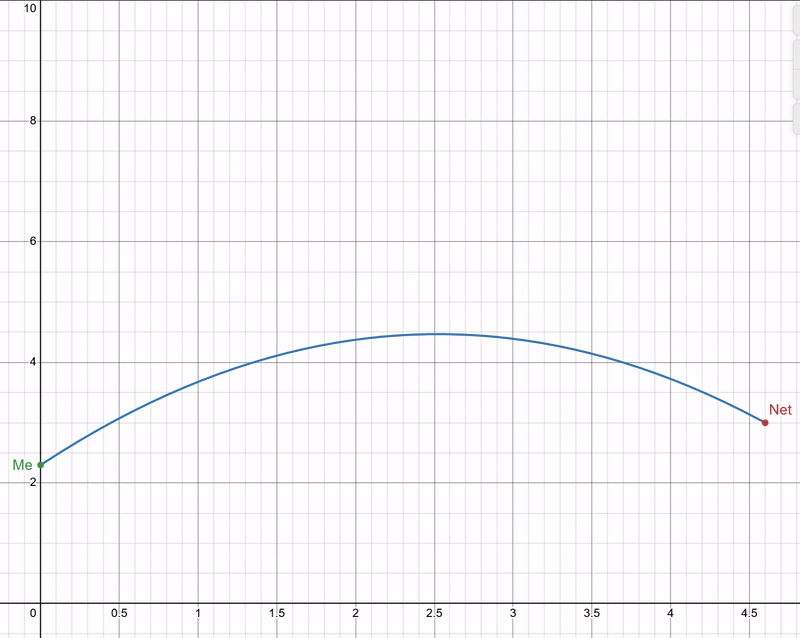
No matter what angle I throw the ball, so long as I throw it sufficiently hard enough it will always go in the net. Common sense if you think about it, but always fun to prove mathematically! So let’s say I want to throw the ball at a 45 degree angle, I can put my value of 45 degrees into my equation (as well as my distance d of 4.6, my displacement s of 3, and my acceleration a of -10) and get a speed output of about 6 m/s!

Perfect! I’ve got everything I need now, so if I head to court, line myself up and throw at a perfect 45 degree angle and throw at exactly 6 m/s…

Perfect! All completely done mathematically and definitely didn’t take me 20 minutes of trying. Now I’ve got that, I can change things up and make them more interesting!

Changing the Variables

Let’s say I’m running towards the net, and I’ve thus increased my horizontal speed? It makes things a little more complicated, but still calculable:

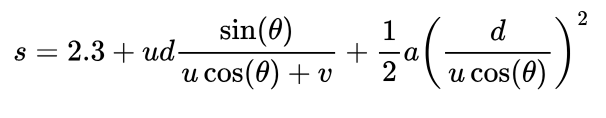
How about instead a further distance, say from that three-point-line. The horizontal distance increases, but the equation stays exactly the same, and thus:

With the power of geometry and mathematics, I have conquered basketball!

With my new found ability, I’ve spent the past week going to the court every evening and throwing from different angles, distances, and speed, making more and more of the shots into the net! Maybe that’s just practice, or maybe knowing the gravity of the situation is what made everything so simple in the end.

*

Thanks for tuning in, I hope you enjoyed this weeks sunday school lesson. I’m pretty tired from shooting hoops all week, especially in the mid 30s temperature that we have here in the south of France. Still, it was an absolute blast to not only get to learn a new sport, but be able to apply my knowledge of maths to it too!

For now I’m going to rest, but I’ll be back with more lessons soon enough!

Au revoir!

Cassie